|
|
|
The
following PID controllers can be optimized by using the excellent PID
auto-tuning software BESTune (see http://bestune.50megs.com/
for details). Theoretically, BESTune is able to optimize any PID controllers,
as long as the PID equations implemented in them are known. In order to include
more PID controllers in BESTune, I am asking you to give me more information
about other well-known brands of industrial PID controllers (brand names, PID
equations implemented, units of the three PID constants, etc). Your help will
be very much appreciated.
In
the following PID equations,
|
CO: |
Controller
Output (also called OutPut and denoted by OP) |
|
PV: |
Process
Variable |
|
SP: |
SetPoint |
|
e=SP-PV |
|
There
are three types of PID controllers: Type A, Type B, and Type C. It is strongly
recommended that type C be used. For more about this, please take a look at http://bestune.50megs.com/typeABC.htm.
A method of desinging type C PID is given at http://bestune.50megs.com/piddesign.htm.
For a quick look at a type C PID loop, take a look at this
picture.
BESTune.Com
Email:
bestune@netzero.net
WWW:
http://bestune.50megs.com/
Standard
Independent PID Controller
There are three types of independent PID control
equations:
|
Type
A: |
|
|
Type
B: |
|
|
Type
C: |
|
We
strongly recommend type C (Unfortunately, most industrial PID controllers use
either type A or type B equations). Differentiating both sides of type C
equation gives:
![]()
Discretization
of the above equation with sampling period Ts gives the following form that can
be implemented in a digital computer:
![]()
where
|
Ts: |
Sampling
period |
seconds |
|
Kp: |
Proportional
gain |
No
unit |
|
Ki: |
Integral
grain |
(1/second) |
|
Kd: |
Derivative
gain |
seconds |
The
last important thing that is often ignored but can never be ignored is to bring
CO back to the upper or lower limit values whenever it is outside these limits,
i.e., whenever CO(k)>CO’s upper limit value, we must set CO(k)=CO’s
upper limit value; and whenever CO(k)<CO’s lower limit value, we must
set CO(k)=CO’s lower limit value.
For
example, if CO(k)=100 means the control valve is 100% open and CO=10 means the
control valve is just closed, then whenever the value of CO(k) calculated by
the above PID equation is larger than 100, we must set CO(k)=100 and whenever
the value of CO(k) calculated by the above PID equation is less than 10, we
must set CO(k)=10.
Standard
Dependent PID Controller
Similarly, there are
also three types of dependent PID equations:
|
Type A: |
|
|
Type B: |
|
|
Type C: |
|
We
strongly recommend type C, i.e.,
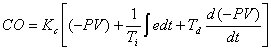
where
|
Kc: |
Proportional
gain |
No
unit |
|
Ti: |
Reset
time |
(min/rep) |
|
Td: |
Rate
time |
(min) |
Allen Bradley
Logix5550 Independent PID
![]()
where
|
Kp: |
Proportional
gain |
No
unit |
|
Ki: |
Integral
gain |
(1/second) |
|
Kd: |
Derivative
gain |
(seconds) |
Allen Bradley
Logix5550 Dependent PID
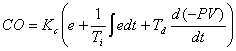
where
|
Kc: |
Proportional
gain |
No
unit |
|
Ti: |
Reset
time |
(min/rep) |
|
Td: |
Rate
time |
(min) |
Allen Bradley
PLC5 Independent PID - Using Integer Blocks
![]()
where
|
Kp: |
Proportional
gain |
(0.01) |
|
Ki: |
Integral
gain |
(0.001/
second) |
|
Kd: |
Derivative
gain |
(seconds) |
Allen Bradley
PLC5 Independent PID - Using PD Blocks
![]()
where
|
Kp: |
Proportional
gain |
No
unit |
|
Ki: |
Integral
gain |
(1/
second) |
|
Kd: |
Derivative
gain |
(seconds) |
Allen Bradley
PLC5 ISA PID - Using Integer Blocks
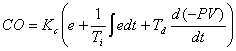
where
|
Kc: |
Proportional
gain |
(0.01) |
|
Ti: |
Reset
time |
(0.01min/rep) |
|
Td: |
Rate
time |
(0.01min) |
Allen Bradley
PLC5 ISA PID - Using PD Blocks
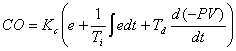
where
|
Kc: |
Proportional
gain |
No
unit |
|
Ti: |
Reset
time |
(min/rep) |
|
Td: |
Rate
time |
(min) |
Allen
Bradley SLC5/02,SLC5/03 and SLC5/04 ISA PID
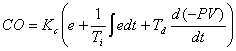
where
|
Kc: |
Proportional
gain |
(0.1) |
|
Ti: |
Reset
time |
(0.1min/rep) |
|
Td: |
Rate
time |
(0.01min) |
Bailey Function
Code FC19 with K=1
![]()
where
|
K: |
Gain
multiplier |
No
unit |
|
Kp: |
Proportional
gain |
No
unit |
|
Ki: |
Integral
reset |
1/min |
|
Kd: |
Derivative
rate action |
Min |
Bailey Function
Code FC156 Independent Form with K=1
![]()
where
|
K: |
Gain
multiplier |
No
unit |
|
Kp: |
Proportional
gain |
No
unit |
|
Ki: |
Integral
reset |
Resets/min |
|
Kd: |
Derivative
rate action |
Min |
Concept PID1 -
PID Controller
The
equivalent continuous time equation the Concept PID1 PID algorithm implements
is:
![]()
where
|
Gain: |
Proportional
gain |
No
unit |
|
TI: |
Reset
time |
(milliseconds) |
|
TD: |
Derivative
Action time |
(milliseconds) |
Concept PID1P - PID Controller with parallel structure
![]()
where
|
KP: |
Proportional
gain |
No
unit |
|
KI: |
Integral
rate |
(1/milliseconds) |
|
KD: |
Differentiation
rate |
(milliseconds) |
Fischer &
Porter DCU 3200 CON Ideal with KP = 1
![]()
If
Kp = 1, the above equation reduces to:
![]()
where
|
KC: |
Gain
constant |
No
unit |
|
TR: |
Reset
time |
(min/rep) |
|
TD: |
Derivative
term |
(min) |
Fischer &
Porter DCU 3200 CON Parallel KP variable with KC=1
![]()
If
KC=1, the above equation reduces to:
![]()
where
|
KP: |
Proportional
gain |
No
unit |
|
TR: |
Reset
time |
(min/rep) |
|
TD: |
Derivative
term |
(min) |
GE Fanuc Series 90-30 and 90-70 Independent Form PID
![]()
where
|
Kp: |
Proportional
gain |
(0.01) |
|
Ki: |
Reset
time |
(0.001rep/second) |
|
Kd: |
Derivative
gain |
(0.01
seconds) |
Hartmann &
Braun Freelance 2000 PID
![]()
where
|
CP: |
Proportional correction value |
No unit |
|
TR: |
Reset time |
(milliseconds) |
|
TD: |
Rate time |
(milliseconds) |
Honeywell TDC
3000 APM Non - Interactive PID
![]()
where
|
K: |
Gain |
No unit |
|
T1: |
Integral time constant |
(min/rep) |
|
T2: |
Derivative time constant |
(min) |
![]()
where
|
PB: |
Proportional
band |
No
unit |
|
|
Integral
mode gain constant |
(0.01min/rep) |
|
K3: |
Derivative
mode gain constant |
(0.01min) |
Siemens S7 PB41
CONT_C PID
![]()
where
|
Gain: |
Proportional
gain |
No
unit |
|
TI: |
Reset
time |
(seconds) |
|
TD: |
Derivative
time |
(seconds) |
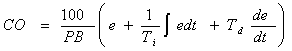
where
|
PB: |
Proportional
band |
No
unit |
|
Ti: |
Integral
time |
(seconds) |
|
Td: |
Derivative
time |
(seconds) |