|
|
|
The following PID controllers can be optimized by using the excellent PID auto-tuning software BESTune (see http://bestune.50megs.com for details). Theoretically, BESTune is able to optimize any PID controllers, as long as the PID equations implemented in them are known. In order to include more PID controllers in BESTune, I am asking you to give me more information about other well-known brands of industrial PID controllers (brand names, PID equations implemented, units of the three PID constants, etc). Your help will be very much appreciated.
The actual PID equations that are implemented inside these
PLCs are all in discrete time or digital form. One example of the discrete time
form of "Allen
Bradley Logix5550 Independent PID
Variable Definition
Allen
Bradley Logix5550 Independent PID
![]()
where
|
Kp: |
Proportional gain |
No unit |
|
Ki: |
Integral gain |
(1/second) |
|
Kd: |
Derivative gain |
(seconds) |
Allen
Bradley Logix5550 Dependent PID
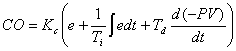
where
|
Kc: |
Proportional gain |
No unit |
|
Ti: |
Reset time |
(min/rep) |
|
Td: |
Rate time |
(min) |
![]()
where
|
Kp: |
Proportional gain |
(0.01) |
|
Ki: |
Integral gain |
(0.001/ second) |
|
Kd: |
Derivative gain |
(seconds) |
![]()
where
|
Kp: |
Proportional gain |
No unit |
|
Ki: |
Integral gain |
(1/ second) |
|
Kd: |
Derivative gain |
(seconds) |
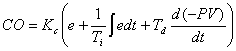
where
|
Kc: |
Proportional gain |
(0.01) |
|
Ti: |
Reset time |
(0.01min/rep) |
|
Td: |
Rate time |
(0.01min) |
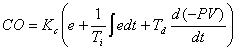
|
Kc: |
Proportional gain |
No unit |
|
Ti: |
Reset time |
(min/rep) |
|
Td: |
Rate time |
(min) |
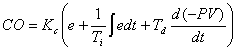
where
|
Kc: |
Proportional gain |
(0.1) |
|
Ti: |
Reset time |
(0.1min/rep) |
|
Td: |
Rate time |
(0.01min) |
![]()
where
|
K: |
Gain multiplier |
No unit |
|
Kp: |
Proportional gain |
No unit |
|
Ki: |
Integral reset |
1/min |
|
Kd: |
Derivative rate action |
Min |
![]()
where
|
K: |
Gain multiplier |
No unit |
|
Kp: |
Proportional gain |
No unit |
|
Ki: |
Integral reset |
Resets/min |
|
Kd: |
Derivative rate action |
Min |
Concept PID1 - PID Controller
![]()
where
|
Gain: |
Proportional gain |
No unit |
|
TI: |
Reset time |
(milliseconds) |
|
TD: |
Derivative Action time |
(milliseconds) |
Concept
PID1P - PID Controller with parallel structure
![]()
|
KP: |
Proportional gain |
No unit |
|
KI: |
Integral rate |
(1/milliseconds) |
|
KD: |
Differentiation rate |
(milliseconds) |
![]()
![]()
where
|
KC: |
Gain constant |
No unit |
|
TR: |
Reset time |
(min/rep) |
|
TD: |
Derivative term |
(min) |
![]()
![]()
where
|
KP: |
Proportional gain |
No unit |
|
TR: |
Reset time |
(min/rep) |
|
TD: |
Derivative term |
(min) |
![]()
where
|
Kp: |
Proportional gain |
(0.01) |
|
Ki: |
Reset time |
(0.001rep/second) |
|
Kd: |
Derivative gain |
(0.01 seconds) |
![]()
|
CP: |
Proportional correction value |
No unit |
|
TR: |
Reset time |
(milliseconds) |
|
TD: |
Rate time |
(milliseconds) |
Honeywell
TDC 3000 APM Non - Interactive PID
![]()
where
|
K: |
Gain |
No unit |
|
T1: |
Integral time constant |
(min/rep) |
|
T2: |
Derivative time constant |
(min) |
![]()
where
|
PB: |
Proportional band |
No unit |
|
K2: |
Integral mode gain constant |
(0.01min/rep) |
|
K3: |
Derivative mode gain constant |
(0.01min) |
![]()
where
|
Gain: |
Proportional gain |
No unit |
|
TI: |
Reset time |
(seconds) |
|
TD: |
Derivative time |
(seconds) |
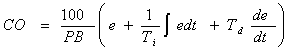
where
|
PB: |
Proportional band |
No unit |
|
Ti: |
Integral time |
(seconds) |
|
Td: |
Derivative time |
(seconds) |